Time series vs. cross-section
Contents
import matplotlib.pyplot as plt
import numpy as np
from statsmodels.tsa.arima_process import arma_acovf
from scipy.linalg import toeplitz
from matplotlib import rc
rc('font',**{'family':'serif','serif':['Palatino']})
rc('text', usetex=True)
plt.rcParams.update({'ytick.left' : True,
"xtick.bottom" : True,
"ytick.major.size": 0,
"ytick.major.width": 0,
"xtick.major.size": 0,
"xtick.major.width": 0,
"ytick.direction": 'in',
"xtick.direction": 'in',
'ytick.major.right': False,
'xtick.major.top': True,
'xtick.top': True,
'ytick.right': True,
'ytick.labelsize': 18,
'xtick.labelsize': 18
})
def correlation_from_covariance(covariance):
v = np.sqrt(np.diag(covariance))
outer_v = np.outer(v, v)
correlation = covariance / outer_v
correlation[covariance == 0] = 0
return correlation
n_obs = 20
arparams = np.array([.80])
maparams = np.array([0])
ar = np.r_[1, -arparams] # add zero-lag and negate
ma = np.r_[1, maparams] # add zero-lag
sigma2=np.array([1])
acov = arma_acovf(ar=ar, ma=ma, nobs=n_obs, sigma2=sigma2)
Sigma = toeplitz(acov)
corr = correlation_from_covariance(Sigma)
tmp = np.random.rand(n_obs, n_obs)
unrestr_cov = np.dot(tmp,tmp.T)
unrestr_mean = np.random.rand(n_obs, 1)
def show_covariance(mean_vec, cov_mat):
K = cov_mat.shape[0]
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(20,8))
m = ax[0].imshow(mean_vec,
cmap='GnBu',
)
K = Sigma.shape[0]
ax[0].set_xticks([])
ax[0].set_xticklabels([]);
ax[0].set_yticks(range(0,K))
ax[0].set_yticklabels(range(1, K+1));
#ax[0].set_xlabel('$\mu$', fontsize=24)
ax[0].set_title('mean', fontsize=24)
c = ax[1].imshow(cov_mat,
cmap="inferno",
)
plt.colorbar(c);
ax[1].set_xticks(range(0,K))
ax[1].set_xticklabels(range(1, K+1));
ax[1].set_yticks(range(0,K))
ax[1].set_yticklabels(range(1, K+1));
ax[1].set_title('Covariance', fontsize=24)
plt.subplots_adjust(wspace=-0.7)
#return (fig, ax)
Time series vs. cross-section¶
sample of households at a point in time (income, expenditure)
aggregate (income, expenditure) over time
dependent vs. independent sampling
\[\begin{split}\begin{bmatrix}Z_1\\Z_2\\Z_3\\\vdots\\Z_K\end{bmatrix} \end{split}\]
\(Z_i\) can be a scalar, or a vector, e.g.
\[\begin{split}Z_i = \begin{bmatrix}y_i\\X_i\end{bmatrix} \end{split}\]
\[ Z \sim \mathcal{N}(\mu, \Sigma) \]
\[\begin{split}\begin{bmatrix}Z_1\\Z_2\\Z_3\\\vdots\\Z_K\end{bmatrix}
\sim \mathcal{N} \left(
\begin{bmatrix}\mu_1\\\mu_2\\\mu_3\\\vdots\\\mu_K\end{bmatrix},
\begin{pmatrix}
\Sigma(1,1) & \Sigma(1,2) & \Sigma(1,3) & \cdots & \Sigma(1,K)\\
\Sigma(2,1) & \Sigma(2,2) & \Sigma(2,3) & \cdots & \vdots\\
\Sigma(3,1) & \Sigma(3,2) & \Sigma(3,3) & \cdots & \vdots\\
\vdots & \vdots & \vdots & \cdots & \vdots\\
\Sigma(K,1) & \cdots & \cdots & \cdots & \Sigma(K,K)\\
\end{pmatrix}
\right)
\end{split}\]
show_covariance(mean_vec=unrestr_mean, cov_mat=unrestr_cov)
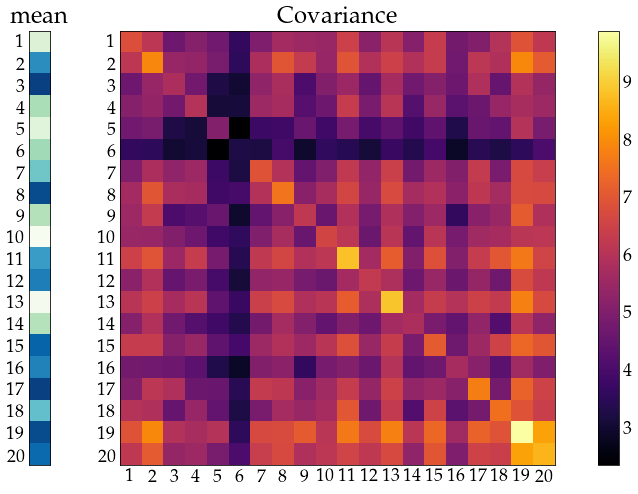
remember: symmetry of \(\Sigma\)
Hopeless without resrtictions - structure on \(\mu, ~\Sigma\)¶
independent
\[\begin{split}\begin{bmatrix}Z_1\\Z_2\\Z_3\\\vdots\\Z_K\end{bmatrix}
\sim \mathcal{N} \left(
\begin{bmatrix}\mu_1\\\mu_2\\\mu_3\\\vdots\\\mu_K\end{bmatrix},
\begin{pmatrix}
\Sigma(1,1) & 0 & 0 & \cdots & 0\\
0 & \Sigma(2,2) & 0 & \cdots & \vdots\\
0 & 0 & \Sigma(3,3) & \cdots & \vdots\\
\vdots & \vdots & \vdots & \cdots & \vdots\\
0 & \cdots & \cdots & \cdots & \Sigma(K,K)\\
\end{pmatrix}
\right)
\end{split}\]
show_covariance(mean_vec=unrestr_mean, cov_mat=np.diagflat(unrestr_cov.diagonal()))
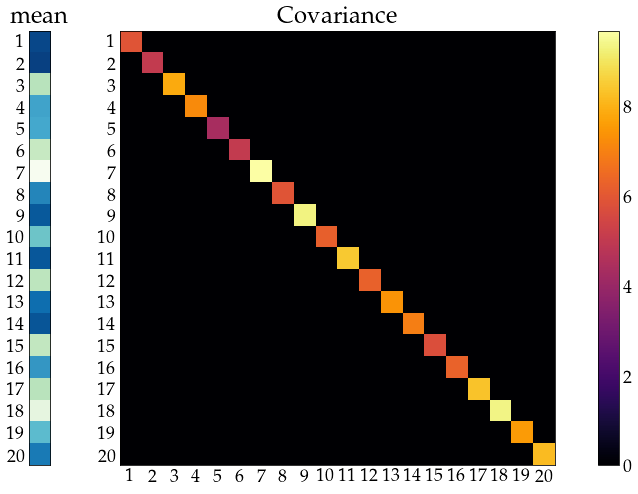
… and identically distributed
\[\begin{split}\begin{bmatrix}Z_1\\Z_2\\Z_3\\\vdots\\Z_K\end{bmatrix}
\sim \mathcal{N} \left(
\begin{bmatrix}\mu\\\mu\\\mu\\\vdots\\\mu\end{bmatrix},
\begin{pmatrix}
\Sigma & 0 & 0 & \cdots & 0\\
0 & \Sigma & 0 & \cdots & \vdots\\
0 & 0 & \Sigma & \cdots & \vdots\\
\vdots & \vdots & \vdots & \cdots & \vdots\\
0 & \cdots & \cdots & \cdots & \Sigma\\
\end{pmatrix}
\right)
\end{split}\]
Note: small \(\mu\) and \(\Sigma\) - not the moments of full joint distribution above
show_covariance(mean_vec=np.ones((n_obs, 1)) ,cov_mat=np.diagflat(Sigma.diagonal()));
time series¶
distribution (\(\mu\), and \(\Sigma\)) is time-invariant (stationarity)
dependence - not too strong and weaker for distant elements (ergodicity)
show_covariance(mean_vec=np.ones((n_obs, 1)) ,cov_mat=Sigma);
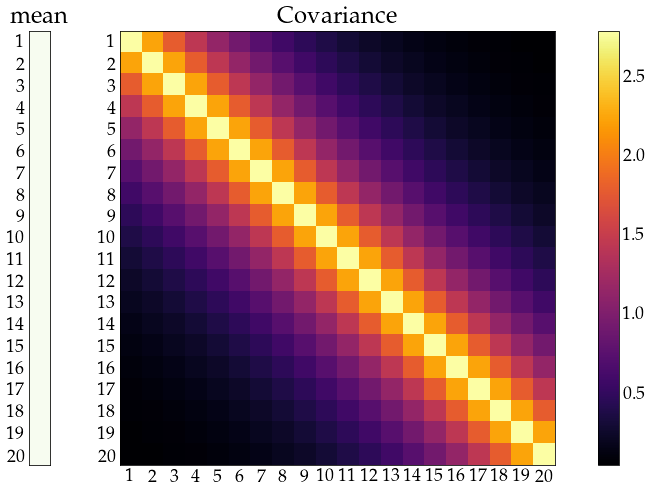
time series models¶
represent temporal dependence in a parsimonious way
AR (1) model:
\[z_t = \alpha z_{t-1} + \varepsilon_t\]MA(1) model:
\[z_t = \varepsilon_t + \psi \varepsilon_{t-1}\]ARMA(1,1) model:
\[z_t = \alpha z_{t-1} + \varepsilon_t + \psi \varepsilon_{t-1}\]etc.
represent temporal interdependence among multiple variables in a parsimonious way
VAR (1) model
VMA(1) model
VARMA(1,1) model
etc.
Consequence of dependence¶
information accumulates more slowly - need different statistical theory to justify methods
forecast the future using the past