ARCH
Contents
ARCH¶
import warnings
warnings.simplefilter("ignore", FutureWarning)
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme()
sns.set_context("notebook")
import pandas as pd
import sqlite3
Conditional heteroskedasticity¶
Time series models are (largely) models of the temporal dependence observed in time series data
the future depends of the past
the past is informative about the future
\[ p(z_{t+h} | z_{t}, z_{t-1}, \cdots) \neq p(z_{t+h})\]
Central objective of time series modeling is characterizing temporal dependence, i.e. characterizing
\[ p(z_{t+h} | z_{t}, z_{t-1}, \cdots) \]
or characterizing some of its moments, such as
\[\begin{split}
\begin{align}
\operatorname{E}(z_{t+h} | z_{t}, z_{t-1}, \cdots) = \operatorname{E}_{t}(z_{t+h}) \\
\operatorname{var}(z_{t+h} | z_{t}, z_{t-1}, \cdots) = \operatorname{var}_{t}(z_{t+h})
\end{align}
\end{split}\]
So far, we have seen models for the conditional mean.
for example, in \(z_t = \alpha z_{t-1} + \varepsilon_t\) the conditional mean is
\[\operatorname{E}(z_{t+1} | z_{t}, z_{t-1}, \cdots) = \operatorname{E}(z_{t+1} | z_{t}) = \alpha z_t \]
changes with \(z_t\)
However, the assumptions about \(\varepsilon_t\) imply that \(\operatorname{var}(z_{t+h} | z_{t}, z_{t-1}, \cdots) \) is a constant (independent of \(z_t, z_{t-1}, \cdots\))
for example, in \(z_t = \alpha z_{t-1} + \varepsilon_t\)
\[
\operatorname{var}(z_{t+1} | z_{t}, z_{t-1}, \cdots) = \operatorname{var}(\varepsilon_{t+1} | z_{t}) = \operatorname{var}(\varepsilon_{t+1}) = \sigma^2
\]
independent of \(z_t\)
Gaussian time series model¶
\[
p(\underbrace{z_1, z_2, \cdots, z_T}_{\mathbf{z}_1}, \underbrace{z_{T+1},\cdots, z_{T+h}}_{\mathbf{z}_2}) = p(\mathbf{z}_1, \mathbf{z}_2) \sim \mathcal{N}(\boldsymbol \mu, \mathbf{\Sigma}).
\]
Forecasts
\[
p(\mathbf{z}_2 | \mathbf{z}_1) = \mathcal{N}(\boldsymbol \mu_2 + \mathbf{\Sigma}_{2 1} \mathbf{\Sigma}^{-1}_{1 1} (\mathbf{z}_1 - \boldsymbol \mu_1), \mathbf{\Sigma}_{2 2} - \mathbf{\Sigma}_{2 1}\mathbf{\Sigma}_{1 1}^{-1}\mathbf{\Sigma}_{1 2})
\]
\(\operatorname{E}(\mathbf{z}_2 | \mathbf{z}_1) = \boldsymbol \mu_2 + \mathbf{\Sigma}_{2 1} \mathbf{\Sigma}^{-1}_{1 1} (\mathbf{z}_1 - \boldsymbol \mu_1)\;\;\;\;\;\) function of \(\mathbf{z}_1\)
\(\operatorname{cov}(\mathbf{z}_2 | \mathbf{z}_1) = \mathbf{\Sigma}_{2 2} - \mathbf{\Sigma}_{2 1}\mathbf{\Sigma}_{1 1}^{-1}\mathbf{\Sigma}_{1 2}\;\;\;\;\;\;\;\;\;\) constant
More generally, if
\[
\begin{align}
\varepsilon_{t} = z_{t} - \operatorname{E}(z_{t} | z_{t-1}, z_{t-2}, \cdots)
\end{align}
\]
then
\[\operatorname{E}(\varepsilon_{t} | z_{t-1}, z_{t-2}, \cdots) = 0\]
and
\[\operatorname{E}(\varepsilon^2_{t} | z_{t-1}, z_{t-2}, \cdots) = \operatorname{var}(\varepsilon_{t} | z_{t-1}, z_{t-2}, \cdots) = \operatorname{var}(z_{t} | z_{t-1}, z_{t-2}, \cdots)\]
For \(\operatorname{var}(z_{t} | z_{t-1}, z_{t-2}, \cdots)\) to vary with \((z_{t-1}, z_{t-2}, \cdots)\), we need \(\operatorname{var}(\varepsilon_{t} | z_{t-1}, z_{t-2}, \cdots)\) to be a function of \((z_{t-1}, z_{t-2}, \cdots)\)
\[\begin{split}
\begin{align}
\operatorname{var}(\varepsilon_{t} | z_{t-1}, z_{t-2}, \cdots) &= \operatorname{E}(\varepsilon^2_{t} | z_{t-1}, z_{t-2}, \cdots) = h(z_{t-1}, z_{t-2}, \cdots) = \sigma^2_t\\
\end{align}
\end{split}\]
where \(h(.)\) is non-negative
and therefore
\[ \operatorname{var}(z_{t} | z_{t-1}, z_{t-2}, \cdots) = \sigma^2_t\]
conditional heteroskedasticity models are models for \(\sigma^2_t\)
\(\sigma^2_t = \sigma^2\) - homoskedasticity
\(\sigma^2_t \neq \sigma^2\) - heteroskedasticity
Autoregressive conditional heteroskedasticity (ARCH) models¶
ARCH(1)¶
\[\sigma^2_t = \omega_0 + \omega_1 \varepsilon^2_{t-1}\]
\(\omega_0>0\), \(\omega_1 \geq 0 \) (for \(\sigma^2_t\) to be positive)
large shocks (\(\varepsilon_{t-1}\)) are expected to be followed by other large shocks ( large \(\operatorname{var}(\varepsilon_{t} | z_{t-1}, z_{t-2}, \cdots)\) )
Since \(\varepsilon_{t}\) is innovation process (unpredictable)
\[\operatorname{E}_{t-1}(\varepsilon_{t}) = 0\]
we have
\[\operatorname{E}_{t-1}(\varepsilon^2_{t}) = \operatorname{var}_{t-1}(\varepsilon_{t}) = \sigma_t^2= \omega_0 + \omega_1 \varepsilon^2_{t-1}\]
and defining \(\nu_t = \varepsilon^2_{t} - \operatorname{E}_{t-1}(\varepsilon^2_{t}) \)
\[\varepsilon^2_{t}= \omega_0 + \omega_1 \varepsilon^2_{t-1} + \nu_t\]
From
\[\operatorname{E}(\varepsilon_{t} | \varepsilon_{t-1}, \varepsilon_{t-2}, \cdots) = \operatorname{E}(\varepsilon_{t} | z_{t-1}, z_{t-2}, \cdots) = 0\]
and
\[\operatorname{var}(\varepsilon_{t} | \varepsilon_{t-1}, \varepsilon_{t-2}, \cdots) = \operatorname{var}(\varepsilon_{t} | z_{t-1}, z_{t-2}, \cdots) = \omega_0 + \omega_1 \varepsilon^2_{t-1}\]
follows
\[\operatorname{E}(\varepsilon^2_{t} | \varepsilon_{t-1}, \varepsilon_{t-2}, \cdots) = \operatorname{var}(\varepsilon_{t} | \varepsilon_{t-1}, \varepsilon_{t-2}, \cdots) = \sigma_t^2= \omega_0 + \omega_1 \varepsilon^2_{t-1}\]
and
\[\varepsilon^2_{t}= \omega_0 + \omega_1 \varepsilon^2_{t-1} + \nu_t, \;\;\; \text{where} \;\; \nu_t = \varepsilon^2_{t} - \operatorname{E}(\varepsilon^2_{t} | \varepsilon_{t-1}, \varepsilon_{t-2}, \cdots) \]
\[
\nu_t = \varepsilon^2_{t} - \operatorname{E}(\varepsilon^2_{t} | \varepsilon_{t-1}, \varepsilon_{t-2}, \cdots) = \sigma^2_t(\epsilon_t^2 - 1)
\]
\[\varepsilon^2_{t}= \omega_0 + \omega_1 \varepsilon^2_{t-1} + \nu_t\]
AR(1) model for \(\varepsilon^2_{t}\)
\(\varepsilon^2_{t}\) are positively autocorrelated (\(\varepsilon_{t}\) are uncorrelated)
stationarity: \(\omega_1<1\)
unconditional mean of \(\varepsilon^2_{t}\) :
\[ \operatorname{E} \varepsilon^2_{t} = \frac{\omega_0}{1-\omega_1} \]
unconditional variance of \(\varepsilon_{t}\):
\[\operatorname{E} \varepsilon_{t} = 0 \Rightarrow \operatorname{var}(\varepsilon_{t}) = \operatorname{E} \varepsilon^2_{t} = \frac{\omega_0}{1-\omega_1} = \sigma^2\]
\(\varepsilon_{t}\) and \(z_t\) are stationary (unconditional moments are time-invariant)
large (relative to \(\sigma^2\)) shocks expected after large (relative to \(\sigma^2\)) shocks
\[ \varepsilon^2_{t} - \sigma^2 = \omega_0 + \omega_1 (\varepsilon^2_{t-1} - \sigma^2) + \nu_t\]
ARCH(q)¶
\[\sigma^2_t = \omega_0 + \sum_{i}^{q }\omega_i \varepsilon^2_{t-i}\]
as before
\[\varepsilon^2_{t}= \omega_0 + \sum_{i}^{q}\omega_i \varepsilon^2_{t-i} + \nu_t\]
AR(q) model for \(\varepsilon^2_{t}\)
Estimation¶
Pure volatility models¶
\[ z_t = \mu + \varepsilon_t\]
Let
\[e_t \overset{iid}{\sim} (0, 1)\]
Then, we can write
\[\begin{split}
\begin{align}
\varepsilon_t &= \sigma_t e_t\\\\
\end{align}
\end{split}\]
\[\begin{split}
\begin{align}
\varepsilon_t &= \sigma_t \epsilon_t\\\\
& \text{and}\\\\
\frac{z_t}{\sigma_t} &=\epsilon_t
\end{align}
\end{split}\]
if \(e_t \overset{iid}{\sim} \mathcal{N}(0, 1)\) the conditional density of \(z_t\) is
\[
z_t |z_{t-1}, \cdots, z_1 \sim \mathcal{N}(\mu, \sigma^2_t)
\]
because at time \(t-1\), \(\sigma_t\) is known, i.e. a constant
and the conditional log-likelihood of \(z_t\)
\[
\ell_t(\boldsymbol \theta) = -\frac{1}{2}\operatorname{ln}2\pi - \frac{1}{2}\operatorname{ln}\sigma_t - \frac{z_t-\mu}{2 \sigma_t^2}
\]
the likelihood of \(\{z_1, z_2, \cdots, z_{T}\}\)
\[\ell(\boldsymbol \theta | \mathbf{z}) = \sum_{t=1}^{T} \ell_t(\boldsymbol \theta) \]
Time-varying mean¶
\[ z_t = \mu_t + \varepsilon_t\]
\(\mu_t = \operatorname{E}_{t-1} z_t\)
for example
\[\mu_t = \alpha_0 + \alpha_1 z_{t-1}\]
conditional log-likelihood of \(z_t\)
\[
\ell_t(\boldsymbol \theta) = -\frac{1}{2}\operatorname{ln}2\pi - \frac{1}{2}\operatorname{ln}\sigma_t - \frac{z_t-\mu_t}{2 \sigma_t^2}
\]
the likelihood of \(\{z_1, z_2, \cdots, z_{T}\}\)
\[\ell(\boldsymbol \theta | \mathbf{z}) = \sum_{t=1}^{T} \ell_t(\boldsymbol \theta) \]
ARCH models in Python¶
from arch import arch_model
conn = sqlite3.connect(database='FCI_EIKON_long.db')
query ='SELECT * FROM "Eikon-daily" WHERE variable=="STOXXE"'
df = pd.read_sql_query(query, conn)
df = df.set_index('time', drop=True)
df.index = pd.to_datetime(df.index)
df = df.sort_index().dropna()
euro_stoxx = df.drop('variable', axis=1)
euro_stoxx.columns = ['EURO STOXX INDEX']
euro_stoxx_returns = 100 * euro_stoxx.pct_change().dropna()['2004':]
euro_stoxx_returns.columns = ['EURO STOXX Returns']
fig = euro_stoxx_returns.plot(figsize=(14,3), legend=False, title='EURO STOXX Returns', ylabel='%', xlabel='year')
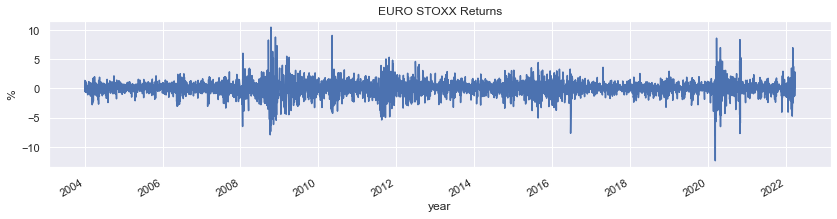
Estimate ARCH(1)¶
arch1 = arch_model(y=euro_stoxx_returns, mean='constant', vol='ARCH')
arch1
Constant Mean(constant: yes,
no. of exog: 0,
volatility: ARCH(p: 1),
distribution: Normal distribution,
ID: 0x2a8f1847f70)
res = arch1.fit(update_freq=0)
print(res.summary())
Optimization terminated successfully (Exit mode 0)
Current function value: 7748.798771475143
Iterations: 6
Function evaluations: 33
Gradient evaluations: 6
Constant Mean - ARCH Model Results
==============================================================================
Dep. Variable: EURO STOXX Returns R-squared: 0.000
Mean Model: Constant Mean Adj. R-squared: 0.000
Vol Model: ARCH Log-Likelihood: -7748.80
Distribution: Normal AIC: 15503.6
Method: Maximum Likelihood BIC: 15523.0
No. Observations: 4749
Date: Mon, Apr 04 2022 Df Residuals: 4748
Time: 17:29:15 Df Model: 1
Mean Model
============================================================================
coef std err t P>|t| 95.0% Conf. Int.
----------------------------------------------------------------------------
mu 0.0424 1.852e-02 2.288 2.212e-02 [6.082e-03,7.869e-02]
Volatility Model
========================================================================
coef std err t P>|t| 95.0% Conf. Int.
------------------------------------------------------------------------
omega 1.2266 7.797e-02 15.731 9.201e-56 [ 1.074, 1.379]
alpha[1] 0.2872 4.632e-02 6.201 5.596e-10 [ 0.196, 0.378]
========================================================================
Covariance estimator: robust
fig = res.plot()
fig.set_figheight(val=8)
fig.set_figwidth(val=14)
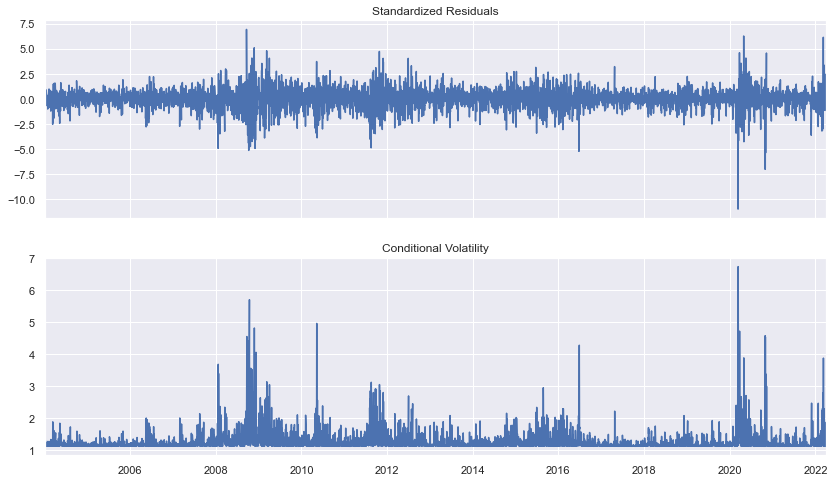
Forecasting¶
forecasts = res.forecast(reindex=False, horizon=12)
forecasts.variance
| h.01 | h.02 | h.03 | h.04 | h.05 | h.06 | h.07 | h.08 | h.09 | h.10 | h.11 | h.12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| time | ||||||||||||
| 2022-03-30 | 1.672126 | 1.706939 | 1.716939 | 1.719811 | 1.720636 | 1.720873 | 1.720941 | 1.720961 | 1.720967 | 1.720968 | 1.720969 | 1.720969 |
forecasts.mean
| h.01 | h.02 | h.03 | h.04 | h.05 | h.06 | h.07 | h.08 | h.09 | h.10 | h.11 | h.12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| time | ||||||||||||
| 2022-03-30 | 0.042386 | 0.042386 | 0.042386 | 0.042386 | 0.042386 | 0.042386 | 0.042386 | 0.042386 | 0.042386 | 0.042386 | 0.042386 | 0.042386 |
from arch.univariate import ARCH
arch7 = arch1
arch7.volatility = ARCH(p=7)
arch7
Constant Mean(constant: yes,
no. of exog: 0,
volatility: ARCH(p: 7),
distribution: Normal distribution,
ID: 0x2a8f1847f70)
res = arch7.fit(update_freq=0)
fig = res.plot()
fig.set_figheight(val=8)
fig.set_figwidth(val=14)
Optimization terminated successfully (Exit mode 0)
Current function value: 7018.71525122455
Iterations: 19
Function evaluations: 216
Gradient evaluations: 19
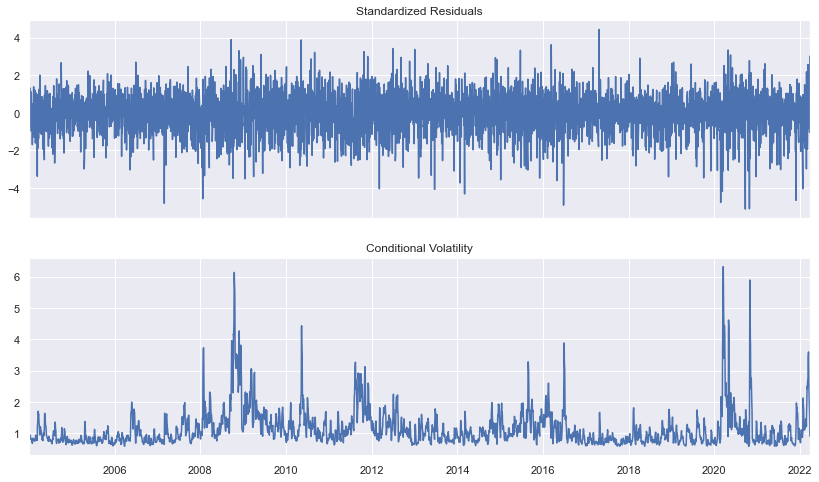
Specifying model for the conditional mean¶
dcpi = pd.read_csv('HICP_unadj_ANR_clean.csv', index_col=0, parse_dates=True)
infl_pt = dcpi[['PT']].copy()
infl_pt.plot(figsize=(12,4), title='Inflation, PT')
<AxesSubplot:title={'center':'Inflation, PT'}, xlabel='date'>
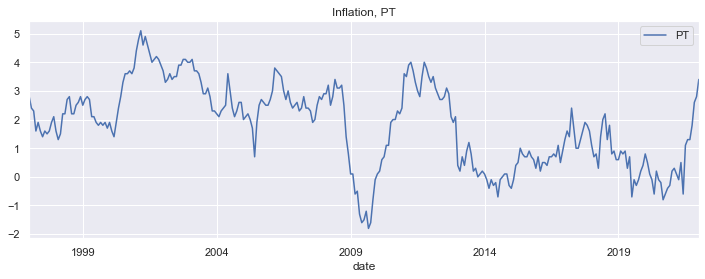
from arch.univariate import ARX
arch_ar_model = ARX(infl_pt,
constant=True,
lags=[1, 12],
volatility=ARCH(p=1))
#arch_ar_model.volatility = ARCH(p=1) # to add volatility if not specified above
arch_ar_model
AR(constant: yes,
lags: 1, 12,
no. of exog: 0,
volatility: ARCH(p: 1),
distribution: Normal distribution,
ID: 0x1f7a54a55d0)
\[z_t = \alpha + \alpha_1 z_{t-1} + \alpha_{12} z_{t-12} + \varepsilon_t \;\;\;\;\; \varepsilon_t \sim \text{ARCH(1)}\]
res_arch_ar_model = arch_ar_model.fit(update_freq=0, disp="off")
print(res_arch_ar_model.summary())
AR - ARCH Model Results
==============================================================================
Dep. Variable: PT R-squared: 0.920
Mean Model: AR Adj. R-squared: 0.919
Vol Model: ARCH Log-Likelihood: -147.565
Distribution: Normal AIC: 305.130
Method: Maximum Likelihood BIC: 323.462
No. Observations: 289
Date: Sun, Apr 03 2022 Df Residuals: 286
Time: 23:43:26 Df Model: 3
Mean Model
===========================================================================
coef std err t P>|t| 95.0% Conf. Int.
---------------------------------------------------------------------------
Const 0.0990 4.107e-02 2.411 1.590e-02 [1.854e-02, 0.180]
PT[1] 1.0056 1.951e-02 51.545 0.000 [ 0.967, 1.044]
PT[12] -0.0646 1.999e-02 -3.232 1.227e-03 [ -0.104,-2.544e-02]
Volatility Model
===========================================================================
coef std err t P>|t| 95.0% Conf. Int.
---------------------------------------------------------------------------
omega 0.1288 1.829e-02 7.039 1.930e-12 [9.291e-02, 0.165]
alpha[1] 0.2623 0.142 1.853 6.389e-02 [-1.515e-02, 0.540]
===========================================================================
Covariance estimator: robust
ar_model = ARX(infl_pt,
constant=True,
lags=[1, 12])
res_ar_model = ar_model.fit(update_freq=0, disp="off")
print(res_ar_model.summary())
AR - Constant Variance Model Results
==============================================================================
Dep. Variable: PT R-squared: 0.920
Mean Model: AR Adj. R-squared: 0.920
Vol Model: Constant Variance Log-Likelihood: -153.943
Distribution: Normal AIC: 315.887
Method: Maximum Likelihood BIC: 330.553
No. Observations: 289
Date: Sun, Apr 03 2022 Df Residuals: 286
Time: 23:43:44 Df Model: 3
Mean Model
==============================================================================
coef std err t P>|t| 95.0% Conf. Int.
------------------------------------------------------------------------------
Const 0.1315 4.353e-02 3.020 2.531e-03 [4.613e-02, 0.217]
PT[1] 0.9882 1.919e-02 51.487 0.000 [ 0.951, 1.026]
PT[12] -0.0574 1.891e-02 -3.037 2.386e-03 [-9.451e-02,-2.038e-02]
Volatility Model
========================================================================
coef std err t P>|t| 95.0% Conf. Int.
------------------------------------------------------------------------
sigma2 0.1699 1.918e-02 8.859 8.041e-19 [ 0.132, 0.207]
========================================================================
Covariance estimator: White's Heteroskedasticity Consistent Estimator
forecasts = res_arch_ar_model.forecast(reindex=False, horizon=6)
forecasts.mean
| h.1 | h.2 | h.3 | h.4 | h.5 | h.6 | |
|---|---|---|---|---|---|---|
| date | ||||||
| 2022-01-01 | 3.498751 | 3.610983 | 3.736772 | 3.82449 | 3.983794 | 4.034121 |
forecasts.variance
| h.1 | h.2 | h.3 | h.4 | h.5 | h.6 | |
|---|---|---|---|---|---|---|
| date | ||||||
| 2022-01-01 | 0.193844 | 0.375625 | 0.555719 | 0.736862 | 0.91979 | 1.104713 |