Forecasting
Contents
Forecasting¶
Time series models are (largely) models of the temporal dependence observed in time series data
the future depends of the past
the past is informative about the future
One motivation behind fitting models to a time series is to forecast future unobserved observations - which would not be possible without a model.
Prediction is interesting for a variety of reasons. First, it is one of the few rationalizations for time-series to be a subject of its own, divorced from economics.
Time series process \(\{z_t \}_{t=-\infty}^{\infty}\)¶
Consider \(z_{T+1}\)
at time \(T\) it is a random variable with some (marginal) distribution
and a conditional distribution, given \(\mathbf{z} = \{z_t \}_{t=1}^{T}\)
describes all knowledge of \(z_{T+1}\) given \(\mathbf{z}\)
called predictive distribution
similarly for \(z_{T+h}\)
Point forecast¶
What is our best guess \(z^{f}_{T+h}\) of \(z_{T+h}\) given information availalbe as of \(T\)?
Depends on how we define “best”, i.e. what the optimality criterion is
if the goal is to minimize the expected (mean) square error
the best point forecast is
for other loss functions, the optimal forecast is another characteristics of the predictive distribution (e.g. the median)
\( p(z_{T+h} | \mathbf{z} ) \) and \(\operatorname{E}(z_{T+h} | \mathbf{z})\) are unknown
we use models to approximate them
Forecasting for AR(1) model¶
at time \(T\) we observe \(z_{1}, z_{2}, \cdots, z_{T}\) and want to forecast \(z_{T+h}\)
\(h = 1\)
why?
the information in past \(z\)’s is the same as information in past \(\varepsilon\)’s, and \(\varepsilon_{T+1}\) is unpredictable
\(h = 2 \)
for any \(h > 0\)
as \(h\longrightarrow \infty\)
first-order Markov process:
\(z_{T+1}\) and \(z_{1:T-1}\) are independent, conditional on \(z_{T}\)
higher-order Markov processes (AR§):
\(z_{T+1}\) and \(z_{1:T-p}\) are independent, conditional on \(z_{T-p+1:T}\)
Mean squared error of the forecasts (MSE)¶
\(h=1\)
\(h>1\)
as \(h\longrightarrow \infty\)
Forecasting for AR§ model¶
\(h = 1\)
for \(h>1\), it is easier to use a VAR(1) representation:
Let \(\mathbf{e} = [1, 0, 0, \cdots, 0]'\) be a \(p\) dimensional vector (first column of a \(p \times p\) identity matrix). Then
and
the MSE of the forecast:
where \(a_i = \mathbf{e}' \boldsymbol A^{i} \mathbf{e} \)
Forecasting for MA(q) and ARMA(p,q) models¶
MA(q)¶
if \(h>q\)
by invertability of MA(q):
import warnings
warnings.simplefilter("ignore", FutureWarning)
warnings.simplefilter("ignore", UserWarning)
from statsmodels.tools.sm_exceptions import ConvergenceWarning
warnings.simplefilter('ignore', ConvergenceWarning)
import numpy as np
from numpy.random import default_rng
from statsmodels.tsa.arima_process import arma_acovf, ArmaProcess
import statsmodels.tsa.api as smt
np.set_printoptions(precision=3, suppress=True)
getting \(\alpha_i\) in Python
beta = np.array([.6, -.3]) # coefficients on e(t-1) and e(t-2)
ar = [1] # coefficient on z_t
ma = np.r_[1, beta]
ma2_process = ArmaProcess(ar, ma)
ma2_process.arma2ar(100)
#statsmodels.tsa.arima_process.arma_impulse_response(ma=[1.0,], ar=[1, .6, -.3], leads=10)
array([ 1. , -0.6 , 0.66 , -0.576, 0.544, -0.499, 0.462, -0.427,
0.395, -0.365, 0.338, -0.312, 0.289, -0.267, 0.247, -0.228,
0.211, -0.195, 0.18 , -0.167, 0.154, -0.142, 0.132, -0.122,
0.112, -0.104, 0.096, -0.089, 0.082, -0.076, 0.07 , -0.065,
0.06 , -0.055, 0.051, -0.047, 0.044, -0.041, 0.037, -0.035,
0.032, -0.03 , 0.027, -0.025, 0.023, -0.022, 0.02 , -0.018,
0.017, -0.016, 0.015, -0.014, 0.012, -0.012, 0.011, -0.01 ,
0.009, -0.008, 0.008, -0.007, 0.007, -0.006, 0.006, -0.005,
0.005, -0.005, 0.004, -0.004, 0.004, -0.003, 0.003, -0.003,
0.003, -0.002, 0.002, -0.002, 0.002, -0.002, 0.002, -0.001,
0.001, -0.001, 0.001, -0.001, 0.001, -0.001, 0.001, -0.001,
0.001, -0.001, 0.001, -0.001, 0.001, -0. , 0. , -0. ,
0. , -0. , 0. , -0. ])
the MSE of forecast:
h = 2
If \(\operatorname{E}_{T} \varepsilon_{T} \approx \varepsilon_{T}\), \(\operatorname{E}_{T} \varepsilon_{T-1} \approx \varepsilon_{T-1}\), etc:
general \(h\)
ARMA(p, q)¶
obtain \(\operatorname{E}_{T} \varepsilon_{T}\), \(\operatorname{E}_{T} \varepsilon_{T-1}\) etc as in the MA(q) case
alpha = np.array([.8])
beta = np.array([0.1])
ar = np.r_[1, -alpha] # coefficient on z(t) and z(t-1)
ma = np.r_[1, beta] # coefficients on e(t) and e(t-1)
arma11_process = ArmaProcess(ar, ma)
arma11_process.arma2ar(8)
array([ 1. , -0.9 , 0.09 , -0.009, 0.001, -0. , 0. , -0. ])
Using the \(MA(\infty)\) representation:
we have $$
$$
the MSE of forecast :
assuming (as for MA(q)) \(\operatorname{E}_{T} \varepsilon_{T} \approx \varepsilon_{T}\), \(\operatorname{E}_{T} \varepsilon_{T-1} \approx \varepsilon_{T-1}\), etc:
in general \(\operatorname{E}(z_{T+h} | \mathbf{z}) \) is unknown and non-linear function of \(\mathbf{z}\)
Gaussian time series model¶
Then,
\(\operatorname{E}(\mathbf{z}_2 | \mathbf{z}_1) = \boldsymbol \mu_2 + \mathbf{\Sigma}_{2 1} \mathbf{\Sigma}^{-1}_{1 1} (\mathbf{z}_1 - \boldsymbol \mu_1)\;\;\;\;\;\) optimal forecast
\(\operatorname{cov}(\mathbf{z}_2 | \mathbf{z}_1) = \mathbf{\Sigma}_{2 2} - \mathbf{\Sigma}_{2 1}\mathbf{\Sigma}_{1 1}^{-1}\mathbf{\Sigma}_{1 2}\;\;\;\;\;\;\;\;\;\) MSE of the optimal forecast
we can restrict “best” to apply to linear functions only: best linear predictor of \(z_{T+h}\) given \(\mathbf{z}\)
if the loss is the MSE, the best linear predictor is (1) with
Prediction operator¶
the best linear prediction of random variable \(y\) given a random vector \(\mathbf{z}\)
has lowest MSE loss
the MSE of \(\operatorname{P}(y|\mathbf{z})\):
properties of \(\operatorname{P}(y|\mathbf{z})\) :
\(\operatorname{E} \left(y - \operatorname{P}(y|\mathbf{z}) \right) = 0\)
\(\operatorname{E} \left((y - \operatorname{P}(y|\mathbf{z}))\mathbf{z} \right) = 0\)
\(\operatorname{P}\left(z_i|\mathbf{z}) \right) = z_i\)
\(\operatorname{P}\left(y|\mathbf{z}) \right) = \operatorname{E} y\), if \(\operatorname{cov}(y,\mathbf{z})=0\)
ARMA forecasting in Python¶
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima.model import ARIMA
from numpy.random import default_rng
generate data from ARMA(1,1)
gen = default_rng(100)
T=700
z = arma11_process.generate_sample(T, distrvs=gen.normal)
estimate
arma_model = ARIMA(z, order=(1, 0, 1), trend="n")
arma_results = arma_model.fit()
print(arma_results.summary())
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 700
Model: ARIMA(1, 0, 1) Log Likelihood -998.176
Date: Mon, 21 Mar 2022 AIC 2002.351
Time: 10:22:36 BIC 2016.005
Sample: 0 HQIC 2007.629
- 700
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.8075 0.027 29.733 0.000 0.754 0.861
ma.L1 0.0199 0.047 0.423 0.672 -0.072 0.112
sigma2 1.0126 0.058 17.456 0.000 0.899 1.126
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 2.05
Prob(Q): 0.98 Prob(JB): 0.36
Heteroskedasticity (H): 1.06 Skew: 0.06
Prob(H) (two-sided): 0.66 Kurtosis: 2.76
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
forecast the next 5 values
arma_results.forecast(steps=5)
array([-0.816, -0.659, -0.532, -0.43 , -0.347])
get forecasts and CI
fcast_res = arma_results.get_forecast(steps=5,)
fcast_res.summary_frame()
| y | mean | mean_se | mean_ci_lower | mean_ci_upper |
|---|---|---|---|---|
| 0 | -0.815737 | 1.006267 | -2.787985 | 1.156510 |
| 1 | -0.658719 | 1.306041 | -3.218512 | 1.901073 |
| 2 | -0.531925 | 1.468926 | -3.410966 | 2.347116 |
| 3 | -0.429537 | 1.566040 | -3.498920 | 2.639846 |
| 4 | -0.346857 | 1.626246 | -3.534241 | 2.840527 |
working with dates
data = pd.DataFrame(z, index=pd.date_range(start='1964', freq='M', periods=T), columns=['z'])
data.tail()
| z | |
|---|---|
| 2021-12-31 | -1.983945 |
| 2022-01-31 | -3.883839 |
| 2022-02-28 | -2.971514 |
| 2022-03-31 | -2.339958 |
| 2022-04-30 | -1.031274 |
arma_model = ARIMA(data, order=(1, 0, 1), trend="n")
arma_results = arma_model.fit()
fcast_res = arma_results.get_forecast(steps=24)
fcast = fcast_res.summary_frame()
fcast.head()
| z | mean | mean_se | mean_ci_lower | mean_ci_upper |
|---|---|---|---|---|
| 2022-05-31 | -0.815737 | 1.006267 | -2.787985 | 1.156510 |
| 2022-06-30 | -0.658719 | 1.306041 | -3.218512 | 1.901073 |
| 2022-07-31 | -0.531925 | 1.468926 | -3.410966 | 2.347116 |
| 2022-08-31 | -0.429537 | 1.566040 | -3.498920 | 2.639846 |
| 2022-09-30 | -0.346857 | 1.626246 | -3.534241 | 2.840527 |
plot forecasts
fig, ax = plt.subplots(figsize=(15, 5))
# Plot the data (here we are subsetting it to get a better look at the forecasts)
data.loc['2018':].plot(ax=ax)
# Construct the forecasts
fcast['mean'].plot(ax=ax, style='k--')
ax.fill_between(fcast.index, fcast['mean_ci_lower'], fcast['mean_ci_upper'], color='k', alpha=0.1);
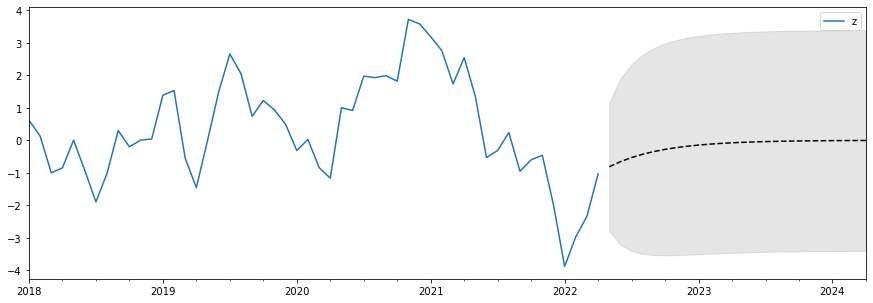
In-sample forecast evaluation¶
use
as an estimate of the MSE
data['forecast'] = arma_results.forecasts.flatten()
data['forecast errors'] = arma_results.forecasts_error.flatten()
data.tail()
| z | forecast | forecast errors | |
|---|---|---|---|
| 2021-12-31 | -1.983945 | -0.373014 | -1.610931 |
| 2022-01-31 | -3.883839 | -1.634070 | -2.249770 |
| 2022-02-28 | -2.971514 | -3.180953 | 0.209439 |
| 2022-03-31 | -2.339958 | -2.395378 | 0.055420 |
| 2022-04-30 | -1.031274 | -1.888448 | 0.857174 |
(arma_results.forecasts_error**2).sum()/T
1.0138467224702907
arma_results.mse
1.0138467224702907
In-sample forecasts are based on model estimated using the full sample
in AR(1) model
introduces information from the future relative to the time (\(t<T\)) when forecasts are produced
Out-of-sample (OOS) forecast evaluation¶
parameter estimates of the forecasting model use only information available at the time when the forecast is computed
fit the model on a training sample \(z_1, \cdots, z_t\) for some \(t=t_0<T\)
produce forecast \(\hat{z}^{f}_{t+1}\) from the end of that sample
compare to true value \(z_{t+1}\)
expand the sample to include the next observation, and repeat until \(t=T-1\)
The OOS estimate of MSE
data = data[['z']]
# Setup forecasts
nforecasts = 1
forecasts = {}
# Get the number of initial training observations
nobs = len(data)
n_init_training = int(nobs * 0.8)
# Create model for initial training sample, fit parameters
init_training_endog = data.iloc[:n_init_training]
mod = ARIMA(init_training_endog, order=(1, 0, 1), trend="n")
res = mod.fit()
# Save initial forecast
forecasts[init_training_endog.index[-1]] = res.forecast(steps=nforecasts)
# Step through the rest of the sample
for t in range(n_init_training, nobs-1):
# Update the results by appending the next observation
updated_data = data.iloc[t:t+1]
res = res.append(updated_data, refit=True)
# Save the new set of forecasts
forecasts[updated_data.index[0]] = res.forecast(steps=nforecasts)
# Combine all forecasts into a dataframe
forecasts = pd.concat(forecasts, axis=1)
forecasts.iloc[:5, :5]
| 2010-08-31 | 2010-09-30 | 2010-10-31 | 2010-11-30 | 2010-12-31 | |
|---|---|---|---|---|---|
| 2010-09-30 | 1.632432 | NaN | NaN | NaN | NaN |
| 2010-10-31 | NaN | 0.928112 | NaN | NaN | NaN |
| 2010-11-30 | NaN | NaN | 0.127096 | NaN | NaN |
| 2010-12-31 | NaN | NaN | NaN | 1.271923 | NaN |
| 2011-01-31 | NaN | NaN | NaN | NaN | 0.60945 |
forecasts.iloc[-5:, -5:]
| 2021-11-30 | 2021-12-31 | 2022-01-31 | 2022-02-28 | 2022-03-31 | |
|---|---|---|---|---|---|
| 2021-12-31 | -0.373446 | NaN | NaN | NaN | NaN |
| 2022-01-31 | NaN | -1.62698 | NaN | NaN | NaN |
| 2022-02-28 | NaN | NaN | -3.185304 | NaN | NaN |
| 2022-03-31 | NaN | NaN | NaN | -2.400559 | NaN |
| 2022-04-30 | NaN | NaN | NaN | NaN | -1.891933 |
# Construct the forecast errors
forecast_errors = {}
for c in forecasts.columns:
forecast_errors[c] = data.iloc[n_init_training:, 0] - forecasts.loc[:,c]
forecast_errors = pd.DataFrame.from_dict(forecast_errors)
def flatten(column):
return column.dropna().reset_index(drop=True)
flattened = forecast_errors.apply(flatten)
flattened.index = (flattened.index + 1).rename('horizon')
flattened.T.head()
| horizon | 1 |
|---|---|
| 2010-08-31 | -0.496213 |
| 2010-09-30 | -0.757934 |
| 2010-10-31 | 1.392945 |
| 2010-11-30 | -0.523532 |
| 2010-12-31 | -0.075812 |
forecast_errors = flattened.T.dropna().values.flatten()
# Compute the root mean square error
rmse = (forecast_errors**2).mean()**0.5
print(rmse)
1.0117784839655213
