.ipynb .pdf

Binder

Contents

Appilcations of state space models

ARMA(p,q) models

Example

MA(1)

\[ z_{t} = \varepsilon_{t} + \beta \varepsilon_{t-1} \]

State space form

\[\begin{split} \begin{align} \left[\begin{array}{c} \varepsilon_{t}\\ \varepsilon_{t-1}\\ \end{array}\right] &= \begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} \left[\begin{array}{c} \varepsilon_{t-1}\\ \varepsilon_{t-2}\\ \end{array}\right] + \left[\begin{array}{c} \varepsilon_{t}\\ 0\\ \end{array}\right] \\\\ z_t & = \left[\begin{array}{cc} 1 \; \beta \end{array} \right] \left[\begin{array}{c} \varepsilon_{t}\\ \varepsilon_{t-1}\\ \end{array}\right] \end{align} \end{split}\]

Example ARMA(2,1)

\[ z_{t} = \alpha_1 z_{t-1} + \alpha_2 z_{t-2} + \varepsilon_{t} + \beta \varepsilon_{t-1} \]

State space form

\[\begin{split} \begin{align} \left[\begin{array}{c} x_{1,t}\\ x_{2,t}\\ \end{array}\right] &= \begin{bmatrix} \alpha_1 & \alpha_2 \\ 1 & 0 \end{bmatrix} \left[\begin{array}{c} x_{1,t-1}\\ x_{2,t-1}\\ \end{array}\right] + \left[\begin{array}{c} \varepsilon_{t}\\ 0\\ \end{array}\right] \\ z_t & = \left[\begin{array}{cc} 1 \; \beta \end{array} \right] \left[\begin{array}{c} x_{1,t}\\ x_{2,t}\\ \end{array}\right] \end{align} \end{split}\]

\[\begin{split} \begin{align} z_t &= \beta(L) x_{1,t}\\ x_{1,t} &= \alpha(L)^{-1} w_{t}\\ \alpha(L)z_t &= \beta(L)w_{t} \end{align} \end{split}\]

Generalizes to ARMA(p,q)

Unobserved-components models

Example

\[\begin{split} \begin{aligned} z_t & = \tau_t + c_t \\ \tau_t & = \tau_{t-1} + \eta_t \\ c_t &= \phi_1 c_{t-1} + \phi_2 c_{t-2} + \varepsilon_t \end{aligned} \end{split}\]

State space form

\[\Delta z_t = \eta_t + \Delta c_t \]

\[\begin{split} \begin{align} \left[\begin{array}{c} c_{t}\\ c_{t-1}\\ \end{array}\right] &= \begin{bmatrix} \phi_1 & \phi_2 \\ 1 & 0 \end{bmatrix} \left[\begin{array}{c} c_{t-1}\\ c_{t-2}\\ \end{array}\right] + \left[\begin{array}{c} \varepsilon_{t}\\ 0\\ \end{array}\right] \\\\ \Delta z_t & = \left[\begin{array}{cc} 1 \; -1 \end{array} \right] \left[\begin{array}{c} c_{t}\\ c_{t-1}\\ \end{array}\right] + \eta_t \\\\ \end{align} \end{split}\]

\[\begin{split} \begin{aligned} z_t & = \tau_t + c_t \\ \tau_t & = \tau_{t-1} + \eta_t \\ c_t &= \phi_1 c_{t-1} + \phi_2 c_{t-2} + \varepsilon_t \end{aligned} \end{split}\]

State space form for the level of \(z_t\)

\[\begin{split} \begin{align} \left[\begin{array}{c} \tau_t\\ c_{t}\\ c_{t-1}\\ \end{array}\right] &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & \phi_1 & \phi_2 \\ 0 & 1 & 0 \end{bmatrix} \left[\begin{array}{c} \tau_{t-1}\\ c_{t-1}\\ c_{t-2}\\ \end{array}\right] + \left[\begin{array}{c} \eta_{t}\\ \varepsilon_{t}\\ \end{array}\right] \\\\ z_t & = \left[\begin{array}{ccc} 1 \; 1 \; 0 \end{array} \right] \left[\begin{array}{c} \tau_t\\ c_{t}\\ c_{t-1}\\ \end{array}\right] \\\\ \end{align} \end{split}\]

Unobserved-components models in Statsmodels

Time-varying parameters

\[\begin{split} \begin{align} z_t &= x_t \beta_t + \varepsilon_t\\ \beta_t &= \beta_{t-1} + \eta_t\\ \end{align} \end{split}\]

Dynamic Factor models

Example

\[\begin{split} \begin{aligned} & \text{observed variables}\\ z_{1,t} & = \lambda_1 f_t + u_{1,t} \\ z_{2,t} & = \lambda_1 f_t + u_{2,t} \\\\ & \text{common factor} \\ f_t & = \alpha f_{t-1} + \eta_t \\\\ & \text{idiosyncratic components} \\ u_{1,t} &= \phi_1 u_{1, t-1} + \varepsilon_{1,t}\\ u_{2,t} &= \phi_2 u_{2, t-1} + \varepsilon_{2,t} \end{aligned} \end{split}\]

State Space form

\[\begin{split} \begin{align} \left[\begin{array}{c} f_t\\ u_{1,t}\\ u_{2,t}\\ \end{array}\right] &= \begin{bmatrix} \alpha & 0 & 0 \\ 0 & \phi_1 & 0 \\ 0 & 0 & \phi_2 \end{bmatrix} \left[\begin{array}{c} f_{t-1}\\ u_{1,t-1}\\ u_{2,t-1}\\ \end{array}\right] + \left[\begin{array}{c} \eta_{t}\\ \varepsilon_{1,t}\\ \varepsilon_{2,t}\\ \end{array}\right] \\\\ \left[\begin{array}{c} z_{1,t}\\ z_{2,t}\\ \end{array}\right] &= \begin{bmatrix} \lambda_1 & 1 & 0 \\ \lambda_2 & 0 & 1 \\ \end{bmatrix} \left[\begin{array}{c} f_t\\ u_{1,t}\\ u_{2,t}\\ \end{array}\right] \end{align} \end{split}\]

• can be extended to multiple factors evolving as VAR(q)

• and more general AR processes for the idiosyncratic components

DFM are a parsimoneous alternative to VARs with many series

Dynamic factor models in Statsmodels

related common trend model

\[\begin{split} \begin{aligned} & \text{observed variables}\\ z_{1,t} & = f_t + u_{1,t} \\ z_{2,t} & = f_t + u_{2,t} \\\\ & \text{common trend} \\ f_t & = f_{t-1} + \eta_t \\\\ & \text{stationary terms} \\ u_{1,t} &= \phi_1 u_{1, t-1} + \varepsilon_{1,t}\\ u_{2,t} &= \phi_2 u_{2, t-1} + \varepsilon_{2,t} \end{aligned} \end{split}\]

State Space form

\[\begin{split} \begin{align} \left[\begin{array}{c} f_t\\ u_{1,t}\\ u_{2,t}\\ \end{array}\right] &= \begin{bmatrix} 1 & 0 & 0 \\ 0 & \phi_1 & 0 \\ 0 & 0 & \phi_2 \end{bmatrix} \left[\begin{array}{c} f_{t-1}\\ u_{1,t-1}\\ u_{2,t-1}\\ \end{array}\right] + \left[\begin{array}{c} \eta_{t}\\ \varepsilon_{1,t}\\ \varepsilon_{2,t}\\ \end{array}\right] \\\\ \left[\begin{array}{c} z_{1,t}\\ z_{2,t}\\ \end{array}\right] &= \begin{bmatrix} \lambda_1 & 1 & 0 \\ \lambda_2 & 0 & 1 \\ \end{bmatrix} \left[\begin{array}{c} f_t\\ u_{1,t}\\ u_{2,t}\\ \end{array}\right] \end{align} \end{split}\]

• \(z_{1,t}\) and \(z_{2,t}\) share a common stochastic trend - cointegrated

• the stationary terms can have more complicated dynamics, and may be correlated (e.g VAR instead of AR processes)

The Hodrick-Prescott filter

\[\begin{split} \begin{aligned} z_t & = \tau_t + c_t \\\\ \underset{\tau_t}{\mathrm{min}} ( \sum_{t=1}^{T}(z_t - \tau_t)^2 & + \lambda \sum_{t=1}^{T}(\tau_{t} - 2\tau_{t-1} + \tau_{t-2})^2 ) \end{aligned} \end{split}\]

Unobserved components model

\[\begin{split} \begin{aligned} z_t & = \tau_t + c_t \\ \tau_t & = \tau_{t-1} + \beta_{t-1}+ \eta_t \\ \beta_t &= \beta_{t-1} + \varepsilon_t \end{aligned} \end{split}\]

State space form

\[\begin{split} \begin{align} \left[\begin{array}{c} \tau_{t}\\ \beta_{t}\\ \end{array}\right] &= \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \left[\begin{array}{c} \tau_{t-1}\\ \beta_{t-1}\\ \end{array}\right] + \left[\begin{array}{c} \eta_{t}\\ \varepsilon_{t}\\ \end{array}\right] \\\\ z_t & = \left[\begin{array}{cc} 1 \; 0 \end{array} \right] \left[\begin{array}{c} \tau_{t}\\ \beta_{t}\\ \end{array}\right] + c_t \\\\ \end{align} \end{split}\]

\[ c_{t} \sim \mathcal{N} \left( 0, \;\mathbf{\sigma}^2_{c}\right),\;\;\;\varepsilon_{t} \sim \mathcal{N} \left( 0, \;\mathbf{\sigma}^2_{\varepsilon}\right),\;\;\; \eta_{t} \sim \mathcal{N} \left( 0, \;\mathbf{\sigma}^2_{\eta}\right) \]

\[ \text{HP-filter restrictions: }\;\;\; \mathbf{\sigma}^2_{\eta} = 0, \;\;\; \frac{\mathbf{\sigma}^2_{c}}{\mathbf{\sigma}^2_{\varepsilon}} = \lambda \]

• no parameters are estimated

• the parameters can be estimated and the restrictions tested

Why You Should Never Use the Hodrick-Prescott Filter

import statsmodels.tsa.api as tsa
from pathlib import Path
import pandas as pd
import matplotlib.pyplot as plt

from fredapi import Fred
fred = Fred(api_key=your_api_key)
start = '1948-01'
end = '2022-01'
df_raw = fred.get_series('GNPC96',  observation_start=start, observation_end=end)
df_raw.index.freq = 'QS'
df_raw.name = 'gdpc1'
df_raw = df_raw.to_frame()
df_raw.head()

	gdpc1
1948-01-01	2102.422
1948-04-01	2137.588
1948-07-01	2149.832
1948-10-01	2152.212
1949-01-01	2122.155

hp_cycle, hp_trend = tsa.filters.hpfilter(df_raw[['gdpc1']], lamb=1600)

mod = tsa.UnobservedComponents(df_raw[['gdpc1']], 'lltrend')
res = mod.smooth([1., 0, 1. / 1600]) # 'sigma2.irregular', 'sigma2.level', 'sigma2.trend'
#print(res.summary())

ucm_trend = pd.Series(res.level.smoothed, index=df_raw[['gdpc1']].index)
fig, ax = plt.subplots(figsize=(16, 8))

ax.plot(df_raw[['gdpc1']], label='real GDP', color='blue', linestyle='solid', linewidth=1)
ax.plot(hp_trend, label='HP trend', color='green', marker='o', linestyle='dashed', linewidth=1, markersize=.5)
ax.plot(ucm_trend, label='UC Model trend', color='red', marker='+', linestyle='dashed', linewidth=1, markersize=.5)
ax.legend();

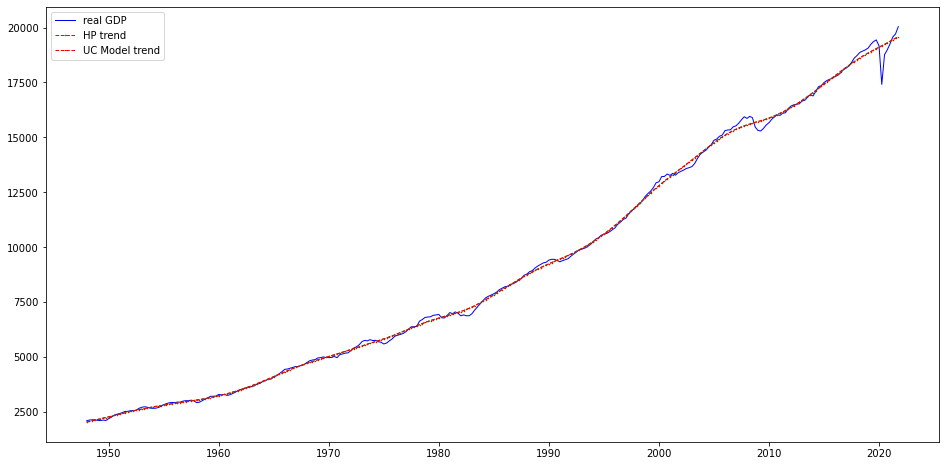
Frequency-domain filters

• time series can be thought of as the sum of periodic functions (fluctuations)

  • frequency domain, spectral analysis of time series

• business cycle components of time series correspond a subset of those fluctuations

  • those with period greater than 1.5 (or 2) years and less than 8 years

  • faster (shorter period) or slower (longer period) fluctuations are interpreted as being outside the business cycle

    • low, business cycle, high frequencies

• frequency-domain filters aim to extract the business cycle components

  • Baxter-King, Christiano-Fitzgerald

periodic functions?

• \(\cos(x) = \cos(x + 2 k \pi), \;\;\; k = 1, 2, \cdots\)

• \(\sin(x) = \sin(x + 2 k \pi), \;\;\; k = 1, 2, \cdots\)

• as function of time: \(\cos(t \omega), \;\;\;t = t_1, \; t_2, \cdots \)

• periodicity means that

\[\begin{split} \begin{align} \cos(\omega t_1) &= \cos(\omega t_h)\\ \\ \omega t_h &= \omega t_1 + 2 \pi \\\\ t_h - t_1 &= \frac{2 \pi}{\omega} \end{align} \end{split}\]

• \(\omega\) is the frequency, \(t_h - t_1\) is the period

• a time series \(z_t\) can be represented as a sum (integral) of

\[\begin{split} \\ \end{split}\]

\[\begin{split} a(\omega) \cos(\omega t) + b(\omega) \sin(\omega t), \;\;\; \omega \in (0, \pi)\\ \end{split}\]

• business cycle component contains only those components with period between 1.5 and 8 years

  • with quarterly data: \(\frac{2 \pi}{32} \leq \omega\leq \frac{2 \pi}{6}\)

  • with monthly data: \(\frac{2 \pi}{96} \leq \omega\leq \frac{2 \pi}{18}\)

• band-pass filter: keep only a subset (band) of \(\omega\)’s in \((0, \pi)\)

• both Baxter-King and Christiano-Fitzgerald filters are computed as weighted moving averages of the series, the difference is in what the weights are

  • symmetric (BK) vs asymmetric (CF) weights

  • truncated on both ends (BK) vs using the full sample (CF)

bk_cycle = tsa.filters.bkfilter(df_raw[['gdpc1']])
cf_cycle, _ = tsa.filters.cffilter(df_raw[['gdpc1']])

cf_cycle.name = 'CF cycle'
bk_cycle.columns = ['BK cycle']
hp_cycle.name = 'HP cycle'

fig = plt.figure(figsize=(14, 10))
ax = fig.add_subplot(111)
cf_cycle.plot(ax=ax, style=["r--", ], legend=True)
bk_cycle.plot(ax=ax, style=["b-", ], legend=True)
hp_cycle.plot(ax=ax, style=["g-.", ], legend=True)

<AxesSubplot:>

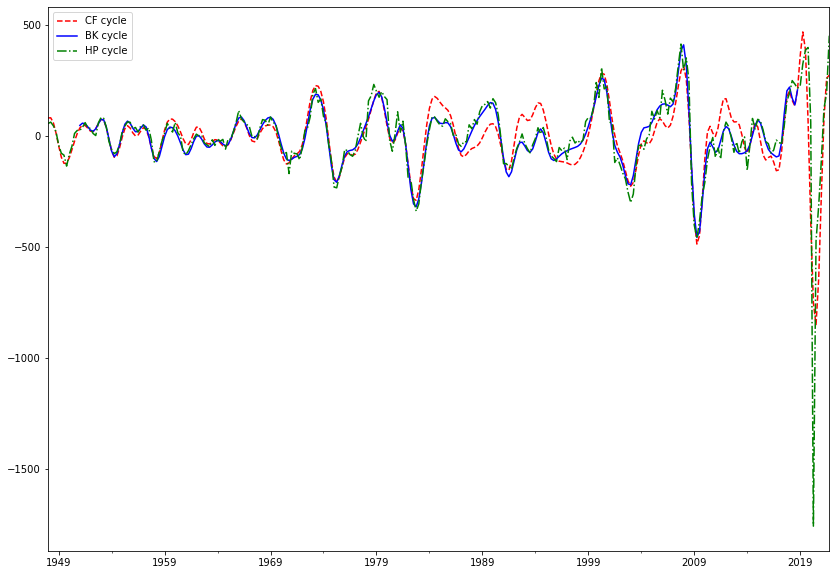
Frequency domain log-likelihood

Whittle log-likelihood

\[\begin{split} \begin{align} \ell(\boldsymbol \theta | \mathbf{z}) & = \sum_{\omega} \ell_{\omega}(\boldsymbol \theta | \mathbf{z}), \;\;\; \omega \in \left(\frac{2 \pi j}{T}, j=1, 2, \cdots, T\right)\\ \\ \ell_{\omega}(\boldsymbol \theta | \mathbf{z}) = -\ln(2 \pi) &- \frac{1}{2} \ln\left(\det(f_{\mathbf{z}}(\omega, \boldsymbol \theta)) \right) - \frac{1}{2} \operatorname{tr}\left(f_{\mathbf{z}}(\omega, \boldsymbol \theta)^{-1} I(\omega, \mathbf{z}) \right) \end{align} \end{split}\]

• \(f_{\mathbf{z}}(\omega, \boldsymbol \theta)\) is the model-implied spectral density of \(\mathbf{z} \) at \(\omega\)

• \(I(\omega, \mathbf{z})\) is the periodogram of \(\mathbf{z}\) at \(\omega\)

• it is like a Gaussian log-likelihood for independent observations

• can be derived by approximating the covariance matrix of \(\mathbf{z}\) by a block circulant matrix, which can be diagonalized using DFT

  \[ \mathbf{z}^{\prime} \mathbf{\Sigma}^{-1}(\mathbf{\theta}) \mathbf{z} \approx \operatorname{tr}\left( \mathbf{z}^{\prime} \mathbf{C}^{-1}(\mathbf{\theta}) \mathbf{z} \right) = \operatorname{tr}\left( \mathbf{z}^{\prime} V^{\prime}\mathbf{F}^{-1}(\mathbf{\theta}) V \mathbf{z} \right) = \sum_{\omega}\operatorname{tr}\left(f(\omega, \boldsymbol \theta)^{-1} I(\omega, \mathbf{z}) \right) \]

Block circulant matrix

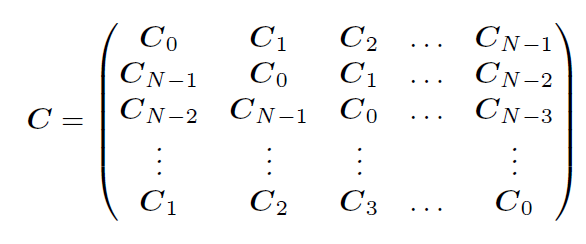
The Whittle log-likelihood can be used as

• an alternative to the Kalman filter

• a way to estimate a model using only a subset of frequencies, e.g. BC frequencies

  • QUANTIFYING CONFIDENCE (2018) by Angeletos, Collard, Dellas

previous

State space models

next

Other topics