Contents

Regime-switching models

import matplotlib.pyplot as plt
import pandas as pd
from fredapi import Fred
fred = Fred(api_key="your_api_key")

start = '1948-01'
end = '2022-01'

unr = fred.get_series('UNRATE',  observation_start=start)
unr.index.freq = unr.index.inferred_freq
unr.name = 'Unemployment'
recessions = fred.get_series('USREC',  observation_start=start, observation_end=end)
recessions.name='recessions'
df = pd.merge(unr, recessions, how='outer', left_index=True, right_index=True)
df = df.fillna(value=0)
df.index.freq = df.index.inferred_freq
dates = df.index._mpl_repr()


indpr = fred.get_series('INDPRO',  observation_start=start, observation_end=end)
indpr.index.freq = indpr.index.inferred_freq
indpr.name = 'Industrial production'
indpr = indpr.to_frame()

Regime-switching models

Motivation

  • empirically, economic contractions are steeper and more short-lived than expansions

fig, ax = plt.subplots(figsize=(12,6))

df[['Unemployment']].plot(ax=ax)
ylim = ax.get_ylim()
ax.fill_between(dates, ylim[0], ylim[1], df[['recessions']].values.flatten(), facecolor='k', alpha=0.1);
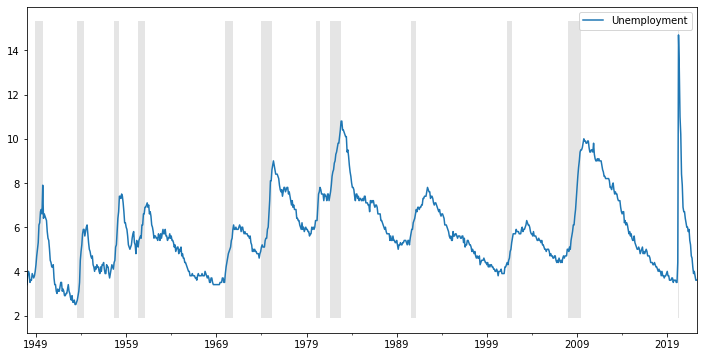
../../_images/01-MS_3_0.png 
fig2, ax = plt.subplots(figsize=(12,6))

indpr.plot(ax=ax)
ylim = ax.get_ylim()
ax.fill_between(dates, ylim[0], ylim[1], df[['recessions']].values.flatten(), facecolor='k', alpha=0.1);
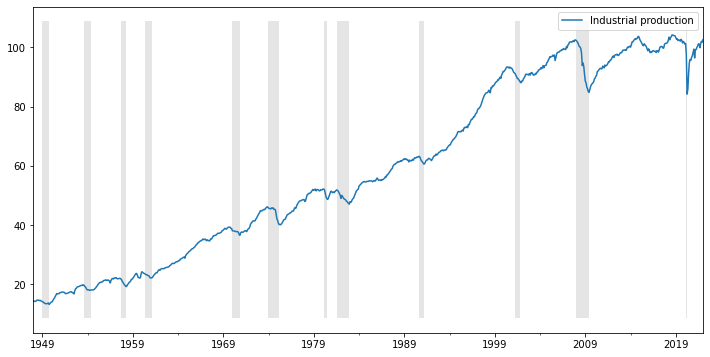
../../_images/01-MS_4_0.png

  • asymmetry between different phases of the business cycle

  • linear models rule out different dynamics of variables during contractions and expansions

  • contractions are much less common part of the sample

    • trend-cycle decompositions based on linear models are better at representing dynamics during expansions.

  • non-linear models may be better at capturing the business cycle asymmetry

  • asymmetry may be explained by different propagation mechanism in contractions vs expansions, or by asymmetry in the shocks

    • capacity constraints, monopoly power, downward vs upward price/wage stickiness, etc

Regime-switching AR§ model

\[\begin{split} \begin{align} \alpha(L) \left( z_t - \mu_t \right) &= \varepsilon_t, \;\;\; \varepsilon_t \sim \mathcal{N} \left( 0, \;\mathbf{\sigma}^2_{t}\right) \\ \\ \mu_t = \mu_0 &+ \mu_1 I(S_t = 1) \\ \\ \sigma^2_t = \sigma^2_0 &+ \sigma^2_1 I(S_t = 1) \\\\ S_t &= 0,1 \;\; (\text{expansion, contraction}) \end{align} \end{split}\]

  • if \(S_t\) is known (observed) this model can be estimated in the usual way by MLE or OLS using dummies

\[\begin{split} \begin{align} \ell(\boldsymbol \theta | \mathbf{z}, \mathbf{S}) & = \sum_{t=1}^{T}\ln(p(z_t | Z_{t-1}, S_t, S_{t-1}, ..., S_{t-p})) \\\\ & \text{if p = 1}\\\\ \ln(p(z_t | Z_{t-1}, S_t, S_{t-1})) &= -\frac{1}{2}\ln(2 \pi \sigma^2_t) - \frac{1}{2 \sigma^2_t}\left( (z_t - \mu_t) - \alpha_1 (y_{t-1} - \mu_{t-1})\right) \end{align} \end{split}\]

  • not very appealing as this assumes regime switches are deterministic - can be predicted

  • if \(S_t\) is unobserved, we cannot condition on \( S_t, S_{t-1}, ..., S_{t-p}\), and have to work with

\[ \begin{align} \ell(\boldsymbol \theta | \mathbf{z}) & = \sum_{t=1}^{T}\ln(p(z_t | Z_{t-1})) \end{align} \]

  • integrate out \(S_t, S_{t-1}\) from the joint density \(p(z_t, S_t, S_{t-1} | Z_{t-1})\) by summing over all possible values of \(S_t\) and \(S_{t-1}\)

\[ \begin{align} p(z_t | Z_{t-1}) &= \sum_{S_t = 0}^{1}\sum_{S_{t-1} = 0}^{1}p(z_t, S_t, S_{t-1} | Z_{t-1}) \end{align} \]

using

\[ p(z_t, S_t, S_{t-1} | Z_{t-1}) = p(z_t | S_t, S_{t-1}, Z_{t-1})\operatorname{Pr}(S_t, S_{t-1} | Z_{t-1}) \]

we have

\[ \begin{align} p(z_t | Z_{t-1}) &= \sum_{S_t = 0}^{1}\sum_{S_{t-1} = 0}^{1} p(z_t | S_t, S_{t-1}, Z_{t-1})\operatorname{Pr}(S_t, S_{t-1} | Z_{t-1}) \end{align} \]

  • \(p(z_t | S_t, S_{t-1}, Z_{t-1})\) computed as before (for known \(S_t\))

Hamilton filter (Hamilton (1989)):

  • assumes time-invariant Markov chain

\[\begin{split} \begin{align} \operatorname{Pr}[S_t = i | S_{t-1} = j, S_{t-2} = k, ..., Z_{t-1}] & = \operatorname{Pr}[S_t = i | S_{t-1} = j]\\ &= p_{ij} \end{align} \end{split}\]

  • what if \(p_{1,1} = 1?\)

  • restrictions?

\[ p_{0, j} + p_{1, j} = 1 \]

  • computes \(\operatorname{Pr}(S_t=i, S_{t-1}=j | Z_{t-1})\) iteratively starting with the unconditional probabilities

\[\begin{split} \begin{align} \operatorname{Pr}(S_1=0) = \frac{1-p_{11}}{2 - p_{11} - p_{00}}, \;\;\; \operatorname{Pr}(S_1=1) = \frac{1-p_{00}}{2 - p_{11} - p_{00}}\\ \end{align} \end{split}\]

Markov-switching models in Statsmodels

Two classes of models:

markov-switching dynamic regression models

\[ z_t = \mu_t + x^{\prime}_t \gamma + y^{\prime}_t \beta_t + \varepsilon_t, \;\;\; \varepsilon_t \sim \mathcal{N} \left( 0, \;\mathbf{\sigma}^2_{t}\right) \]

where both \(x_t\) and \(y_t\) may include lags of \(z_t\)

  • \(z_t\) depends only on the current state (the intercept has 2 possible values for a model with 2 states)

markov-switching autoregression models

\[\begin{split} \begin{align} z_t &= \mu_t + x^{\prime}_t \gamma + y^{\prime}_t \beta_t + \sum_{i=1}^{p}\alpha_{i,t}\left( z_{t-i} - \mu_{t-1} + x^{\prime}_{t-i} \gamma + y^{\prime}_{t-i} \beta_{t-i}\right), \;\;\; \varepsilon_t \sim \mathcal{N} \left( 0, \;\mathbf{\sigma}^2_{t}\right) \\ \\ &\alpha_t(L) \left( z_t - \mu_t - x^{\prime}_t \gamma - y^{\prime}_t \beta_t \right) = \varepsilon_t, \;\;\; \varepsilon_t \sim \mathcal{N} \left( 0, \;\mathbf{\sigma}^2_{t}\right) \end{align} \end{split}\]

  • \(z_t\) depends on the current and past states (the intercept has 4 possible values for a model with 2 states when p=1)

previous

Other topics

next

Granger causality